| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 백준 10828
- 알고리즘
- struct
- UIPanGestureRecognizer
- 컴퓨터 구조
- Reverse Engineering
- Animation
- 표준 템플릿 라이브러리
- 2020.06.14
- SWiFT
- 2020.05.17
- ios
- stl
- NavigationBar
- 모달인듯 모달 아닌 뷰
- 스택
- 순차 컨테이너
- Reversing
- class
- Constraint
- scroll
- Stack
- Swing
- list
- 2020.04.19
- 컴퓨터구조
- 백준 1920
- BOJ
- vector
- UIView
- Today
- Total
야금야금
#2-(1) 컴퓨터 구조 - 컴퓨터 정보의 표현 본문
컴퓨터는 외부에서 들어오는 정보를 0과 1로 표현한다. 그 표현법에 대해 알아보자
비트 Bit : 컴퓨터 정보 표현의 기초 단위이다. 0과 1의 값이 저장되는 가장 작은 저장공간을 말한다.
바이트 Byte : 하나의 영문자 혹은 숫자를 표현하기 위해서는 8개의 비트가 필요하다. 이처럼 하나의 문자를 표현하는 8비트를 1바이트라고 한다. (8bit = 1byte)
워드 Word : 바이트들로 구성된 정보의 단위이다.

진법이란?
: 사용할 수 있는 숫자의 개수와 자리값을 정의해 주는 수 체계이다.
10진법 : 0~9의 10개의 숫자를 이용하여 수를 표현한다. 사람이 일상생활에서 가장 많이 사용하는 수의 체계이다.
2진법 : 0,1을 사용하여 수를 표현한다. 컴퓨터가 사용하는 수의 체계이다.
16진법 : 0~9, A~F를 이용하여 수를 표현한다.
※각 수를 표현하는 기호(0~9, A~F 등)가 기준이 되어 밑 수가 정해진다
ex) 10진수의 밑 수 = 10, 2진수의 밑 수 = 2
[10진수를 부호가 없는 2진수로 표현하기]

10진수 값을 2로 몫이 완전히 나누어질 때까지 연속해서 나눈다.
그 후 매 결과의 나머지 값을 역순으로 읽는다.
왼쪽의 그림에서 십진수인 53은 이진수로 110101이라 나타낸다.
[부호가 없는 2진수를 10진수로 표현하기]
각 자리의 숫자와 자리값을 곱하고 결과들을 모두 더한다.

[부호가 있는 2진 정수 표현]
컴퓨터는 0과 1의 비트를 이용하여 정수를 표현한다. 그렇다면 2진수에서 음의 정수는 어떻게 표현하여야 할까?
2진수의 정수 표현은 3가지로 나타낼 수 있다.
1) 부호화 크기 표현
n비트로 구성된 2진수에서 최상위 비트 즉, 가장 첫 번째의 비트는 수로 부호를 나타낸다. (0일 경우 +, 1일 경우 -)
겉보기에는 부호화 크기 표현을 사용하는 것이 편리해 보이지만 부호화 크기 표현은 0이 두 개 존재한다는 점과 (0 0000000 (= +0)과 1 0000000 (= -0)) 해당 방법으로는 연산에서 실질적인 활용이 불가능하다는 단점이 있다.

위와 같이 자리올림에 따른 덧셈을 진행할 경우 9와 -9를 더해서 -18이라는 엉뚱한 답이 나오게 된다.
보수를 이용한 표현 ( 1의 보수 표현 / 2의 보수 표현 )
우선 보수의 개념부터 살펴보자
보수란?
: 두 수의 합이 진법의 밑 수(10진수면 10, 2진수면 2)가 되게 하는 수를 말한다.
컴퓨터는 덧셈만 가능하고 뺄셈의 개념이 없기 때문에 음수화를 할 경우 보수를 사용한다.
ex) 10진수 3의 보수 = 7 / 10진수 7의 보수 = 3
2) 1의 보수 표현 (쉽게 말해 이진수의 모든 자리 수가 1이 되기 위해 보충해줘야 하는 수)
1의 보수 표현에서 음수화를 할 땐 부호화 크기 표현에서처럼 첫 비트로 부호를 나타내 준다. 그 후 부호가 없는 2진 정수의 모든 비트를 반전시킨다. 1의 보수 표현 또한 0을 00000000과 11111111 두 가지의 방법으로 나타내는 단점이 있다.
3) 2의 보수 표현
2의 보수 표현에서 음수화를 할 땐 1의 보수 표현 결과값에 1을 더한다. 자리올림은 버려 지기 때문에 2의 보수 표현에서 0은 00000000 하나로 정해진다. (자세한 설명은 아래를 확인하자)

n비트 데이터의 표현할 수 있는 수의 범위

n비트의 데이터에서 첫번째 비트를 부호로 사용하기 때문에 숫자를 표현할 수 있는 비트는 n-1개의 비트이다.
각 자리마다 0과 1 두 개의 값이 들어갈 수 있으므로 위와 같이 표현할 수 있는 개수가 주어지는 것이다.
[3비트로 예시를 들어보자]
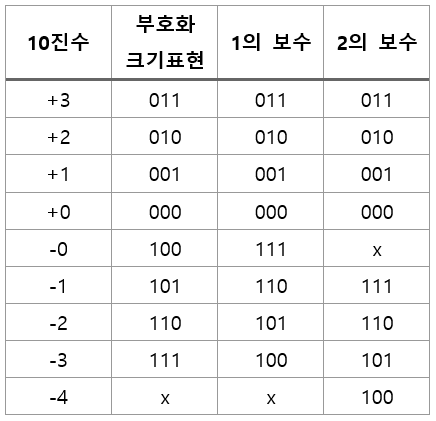
우선 2의 보수에서 0이 한 개만 나올 수 있는 이유를 살펴보자
2의 보수는 1의 보수에 1을 더하여 만든다 1의 보수에서 111로 표현된 0의 경우 1을 더하면 1000으로 사용 가능한 비트 수를 초과하게 된다. 이렇게 한정된 메모리 용량을 넘어가는 것을 오버플로(Over flow)라고 하며 이를 방지하기 위해 덧셈의 결과가 최상위 비트에서 자리 올림이 발생했다면 값을 버리게 된다. 이러한 이유로 2의 보수 표현에서는 0이 한 개만 존재하는 것이다. 0이 한개만 존재하기 때문에 음의 정수를 하나 더 표현할 수 있어 더욱 효율적이다.
이처럼 2의 보수 표현을 사용하면 연산 처리를 단순하고 효율적으로 할 수 있기 때문에 컴퓨터 시스템에서 사용되고 있다.
2진수의 논리 연산
기본 논리 연산
* AND 연산
: 입력값이 모두 1인 경우에만 결과값이 1이 되고 그 외의 경우에는 결과값이 0이 된다.
* OR 연산
: 입력값 중 하나만 1이면 결과값이 1이 되고 입력값이 모두 0일 경우 결과값이 0이 된다.
* XOR 연산 (Exclusive - OR)
: 입력값이 모두 동일한 경우에는 결과값이 0이 되고 그 이외의 경우에는 결과값이 1이 된다.
* NOT 연산
: 주어진 입력값의 반대 값이 결과값이 된다.
응용 논리 연산
선택적 세트(Selective-set) 연산
: 선택된 특정 비트를 1로 세트 시키는 연산
선택적 보수(Selective-complement) 연산
: 선택된 특정 비트를 1의 보수로 비트를 반전시키는 연산
마스크 (Mask) 연산
: 선택된 특정 비트를 0으로 만드는 연산
삽입 (Insert) 연산
: 입력값 내의 특정 위치에 새로운 비트 값들을 삽입하는 연산
비교 (Compare) 연산
: 두 입력값을 비교하는 연산. 같으면 0, 다르면 1을 출력
순환 이동(Circular shift)
: 최상위 혹은 최하위에 있는 비트가 반대편 끝에 있는 비트 위치로 이동해서 비트가 회전하는 이동
산술적 이동 (Arithmetic shift)
: 부호 비트는 유지하고 수의 크기를 나타내는 비트들만 이동
[문제]
참고) 2019 컴퓨터 구조 호준원교수님 강의노트,
디지털논리와 컴퓨터 설계, Harris et al. (조영완 외 번역), 사이텍미디어, 2007,
컴퓨터 구조와 원리 (비주얼 컴퓨터 아키텍처), 신종홍 저, 한빛미디어, 2011
'SWING > 컴퓨터구조' 카테고리의 다른 글
| #4 컴퓨터 구조 - 명령어 형식 (0) | 2020.05.30 |
|---|---|
| #3(2) 컴퓨터 구조 - 메모리 구조 & 레지스터 종류 (0) | 2020.05.23 |
| #3 컴퓨터 구조 - 명령어를 효과적으로 처리하기 위한 기법 (0) | 2020.05.23 |
| #2-(2) 컴퓨터 구조 - 어셈블리 명령어 (0) | 2020.04.18 |
| #1 컴퓨터 시스템의 구성요소 & CPU 구조 및 동작 과정 (0) | 2020.04.12 |




